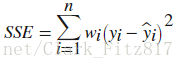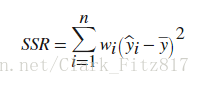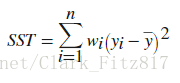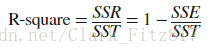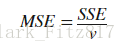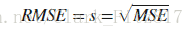工具箱
我的版本是MATLB R2017a,主要介绍曲线拟合与优化工具箱
Curve fitting –> 曲线拟合
曲线函数选项
Exponential:指数逼近,有2种类型, aexp(bx) 、 aexp(bx) + cexp(dx)
Fourier:傅立叶逼近,有7种类型,基础型是 a0 + a1cos(xw) + b1sin(xw)
Gaussian:高斯逼近,有8种类型,基础型是 a1exp(c1-((x-b1)/c1)^2)
Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preserving
Polynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree ~
Power:幂逼近,有2种类型,ax^b 、ax^b + c
Rational:有理数逼近,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~;此外,分子还包括constant型
Smoothing Spline:平滑逼近
Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是 a1sin(b1x + c1)
Weibull:只有一种,abx^(b-1)exp(-a*x^b)
拟合效果评价
除了直观的观察图像和散点的拟合程度外,matlab还提供了几个评价参数
- The sum of squares due to error (SSE)
- R-square
- Adjusted R-square
- Root mean squared error (RMSE)
sse 这个统计量测量的是拟合值与实际值的总偏差和。它也被称为残差的平方求和
值越小,拟合程度越好。
R-square由三个公式计算得来,衡量了拟合在解释数据变化方面的成功程度
越接近1,表示模型在方差中所占的比例更大(with a value closer to 1 indicating that a greater proportion of variance is accounted for by the model)
Adjusted R-square
调整后的R-平方统计量可以接受任何小于或等于1的值,而接近1的值表示更好的拟合。当模型包含无助于预测响应的项时,可能会出现负值。
RMSE
由以下两个公式计算得出
与sse一样,RMSE值越小,拟合程度越好

Optimization –> 优化
利用Matlab的优化工具箱,可以求解线性规划、非线性规划和多目标规划问题。具体而言,包括线性、非线性最小化,最大最小化,二次规划,半无限问题,线性、非线性方程(组)的求解,线性、非线性的最小二乘问题。另外,该工具箱还提供了线性、非线性最小化,方程求解,曲线拟合,二次规划等问题中大型课题的求解方法,为优化方法在工程中的实际应用提供了更方便快捷的途径。
优化工具箱中的函数
优化工具箱中的函数包括下面几类:
1.最小化函数
| 函 数 | 描 述 |
|---|---|
| fgoalattain | 多目标达到问题 |
| fminbnd | 有边界的标量非线性最小化 |
| fmincon | 有约束的非线性最小化 |
| fminimax | 最大最小化 |
| fminsearch, fminunc | 无约束非线性最小化 |
| fseminf | 半无限问题 |
| linprog | 线性课题 |
| quadprog | 二次课题 |
2.方程求解函数
| 函 数 | 描 述 |
|---|---|
| / | 线性方程求解 |
| fsolve | 非线性方程求解 |
| fzero | 标量非线性方程求解 |
3.最小二乘(曲线拟合)函数
| 函 数 | 描 述 |
|---|---|
| / | 线性最小二乘 |
| lsqlin | 有约束线性最小二乘 |
| lsqcurvefit | 非线性曲线拟合 |
| lsqnonlin | 非线性最小二乘 |
| lsqnonneg | 非负线性最小二乘 |
4.实用函数
| 函 数 | 描 述 |
|---|---|
| optimset | 设置参数 |
| optimget |
5.大型方法的演示函数
| 函 数 | 描 述 |
|---|---|
| circustent | 马戏团帐篷问题—二次课题 |
| molecule | 用无约束非线性最小化进行分子组成求解 |
| optdeblur | 用有边界线性最小二乘法进行图形处理 |
6.中型方法的演示函数
| 函 数 | 描 述 |
|---|---|
| bandemo | 香蕉函数的最小化 |
| dfildemo | 过滤器设计的有限精度 |
| goaldemo | 目标达到举例 |
| optdemo | 演示过程菜单 |
| tutdemo | 教程演示 |
参数设置
利用optimset函数,可以创建和编辑参数结构;利用optimget函数,可以获得options优化参数。
● optimget函数
功能:获得options优化参数。
语法:
val = optimget(options,’param’)
val = optimget(options,’param’,default)
描述:
val = optimget(options,’param’) 返回优化参数options中指定的参数的值。只需要用参数开头的字母来定义参数就行了。
val = optimget(options,’param’,default) 若options结构参数中没有定义指定参数,则返回缺省值。注意,这种形式的函数主要用于其它优化函数。
举例:
1. 下面的命令行将显示优化参数options返回到my_options结构中:
val = optimget(my_options,’Display’)
2. 下面的命令行返回显示优化参数options到my_options结构中(就象前面的例子一样),但如果显示参数没有定义,则返回值’final’:
optnew = optimget(my_options,’Display’,’final’);
参见:
optimset
● optimset函数
功能:创建或编辑优化选项参数结构。
语法:
options = optimset(‘param1’,value1,’param2’,value2,…)
optimset
options = optimset
options = optimset(optimfun)
options = optimset(oldopts,’param1’,value1,…)
options = optimset(oldopts,newopts)
描述:
options = optimset(‘param1’,value1,’param2’,value2,…) 创建一个称为options的优化选项参数,其中指定的参数具有指定值。所有未指定的参数都设置为空矩阵[](将参数设置为[]表示当options传递给优化函数时给参数赋缺省值)。赋值时只要输入参数前面的字母就行了。
optimset函数没有输入输出变量时,将显示一张完整的带有有效值的参数列表。
options = optimset (with no input arguments) 创建一个选项结构options,其中所有的元素被设置为[]。
options = optimset(optimfun) 创建一个含有所有参数名和与优化函数optimfun相关的缺省值的选项结构options。
options = optimset(oldopts,’param1’,value1,…) 创建一个oldopts的拷贝,用指定的数值修改参数。
options = optimset(oldopts,newopts) 将已经存在的选项结构oldopts与新的选项结构newopts进行合并。newopts参数中的所有元素将覆盖oldopts参数中的所有对应元素。
举例:
1.下面的语句创建一个称为options的优化选项结构,其中显示参数设为’iter’,TolFun参数设置为1e-8:
options = optimset(‘Display’,’iter’,’TolFun’,1e-8)
2.下面的语句创建一个称为options的优化结构的拷贝,改变TolX参数的值,将新值保存到optnew参数中:
optnew = optimset(options,’TolX’,1e-4);
3.下面的语句返回options优化结构,其中包含所有的参数名和与fminbnd函数相关的缺省值:
options = optimset(‘fminbnd’)
4.若只希望看到fminbnd函数的缺省值,只需要简单地键入下面的语句就行了:
optimset fminbnd
或者输入下面的命令,其效果与上面的相同:
optimset(‘fminbnd’)
参见:
optimget
模型输入时需要注意的问题
使用优化工具箱时,由于优化函数要求目标函数和约束条件满足一定的格式,所以需要用户在进行模型输入时注意以下几个问题:
1.目标函数最小化
优化函数fminbnd、fminsearch、fminunc、fmincon、fgoalattain、fminmax和lsqnonlin都要求目标函数最小化,如果优化问题要求目标函数最大化,可以通过使该目标函数的负值最小化即-f(x)最小化来实现。近似地,对于quadprog函数提供-H和-f,对于linprog函数提供-f。
2.约束非正
优化工具箱要求非线性不等式约束的形式为Ci(x)≤0,通过对不等式取负可以达到使大于零的约束形式变为小于零的不等式约束形式的目的,如Ci(x)≥0形式的约束等价于- Ci(x)≤0;Ci(x)≥b形式的约束等价于- Ci(x)+b≤0。
3.避免使用全局变量
@(函数句柄)函数
MATLAB6.0中可以用@函数进行函数调用。@函数返回指定MATLAB函数的句柄,其调用格式为:
handle = @function
利用@函数进行函数调用有下面几点好处:
● 用句柄将一个函数传递给另一个函数;
● 减少定义函数的文件个数;
● 改进重复操作;
● 保证函数计算的可靠性。
下面的例子为humps函数创建一个函数句柄,并将它指定为fhandle变量。
fhandle = @humps;
同样传递句柄给另一个函数,也将传递所有变量。本例将刚刚创建的函数句柄传递给fminbnd函数,然后在区间[0.3,1]上进行最小化。
x = fminbnd (@humps, 0.3, 1)
x =
0.6370